
Monopoly, ironically enough, had anticapitalist origins.Michael Mechanic
A version of this article was originally published on the author’s website.
In November 2019, not long before the pandemic put the kibosh on indoor socializing, my wife and I had some friends over for dinner and what turned out to be a fateful game of Yahtzee.
Monopoly has a bit of strategy, whereas Yahtzee is mostly luck, but it struck me—as I’d been researching a book about wealth and inequality—that both of these popular parlor games are idealized representations of capitalism. Idealized in that each player starts with the same likelihood of success. Yet in both games, once a player achieves a significant lead, the rewards multiply so fast that it becomes hard for others to compete. How long are you gonna last against the guy who owns all the railroads and has hotels on Broadway and Park Place?
In Yahtzee, you roll five dice—keeping the ones you like and re-rolling the rest up to twice more—as you go for certain combinations. The most valuable roll is a “Yahtzee” (five of a kind), worth 50 points. Assuming you try for a Yahtzee only when you get three of a kind or better on the first roll, the odds that you will get at least one Yahtzee in a game (13 turns) are just over 1 in 4. (See appendix for the calculations.)
But every subsequent Yahtzee is worth double: 100 points! Two Yahtzees makes you extremely hard to beat—the odds of that are about 1 in 23. The chance of hitting three is 1 in 143. On this particular night, I rolled four!
It was like winning the lottery—except that the odds of rolling four Yahtzees are 1 in 250, slightly better than the 1-in-292 million odds of winning Powerball’s grand prize. Even so, by my third Yahtzee, the other players were mere peasants, whereas I was the Dice King, reaping the rewards of my earlier dumb luck.
In Paul Piff’s memorable Monopoly experiment, the subject of this Atlantic book excerpt, the psychologist rigged a series of games from the outset and watched the “rich players,” as determined by a coin toss, grow increasingly arrogant and aggressive as they amassed more and more fictional real-estate wealth.
With Piff’s observations in mind, I resolved to remain humble. But the peasants, my wife included, turned on me. They threw shade, and when I tried to respond, rolled their eyes: Whatever, dude. The pitchforks were out and sharpened. Such is a paradox of wealth in America. We want it, yet we feel resentment toward those who have it—even in a dumb game.
From a competition perspective, Yahtzee’s scoring makes no sense. If you roll one Yahtzee, you’re on a path to victory. If you roll two or three, game over. Why create rules that give a huge advantage to the player who’s already winning? (One might ask Congress that question.)
I read up on the game’s origins. Originally called “The Yacht Game,” Yahtzee was invented in 1954 by a wealthy Canadian couple to pass the time aboard—you’ll never believe it—their yacht! The game grew so popular within their elite circles that they approached Edwin Lowe, a man who’d made his fortune in the 1920s by transforming Beano, an old carnival game, into the best-selling game we know as Bingo. The Canadian yachters would have been well aware of the advantages society bestows upon those of us who have already rolled a few Yahtzees in life.
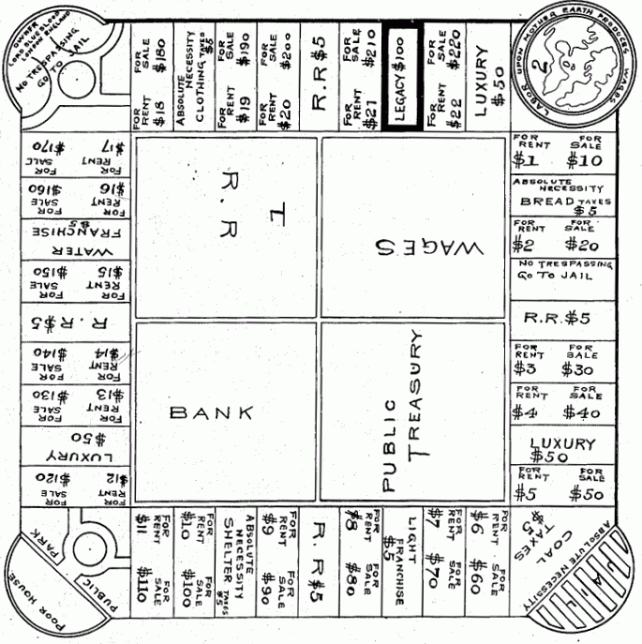
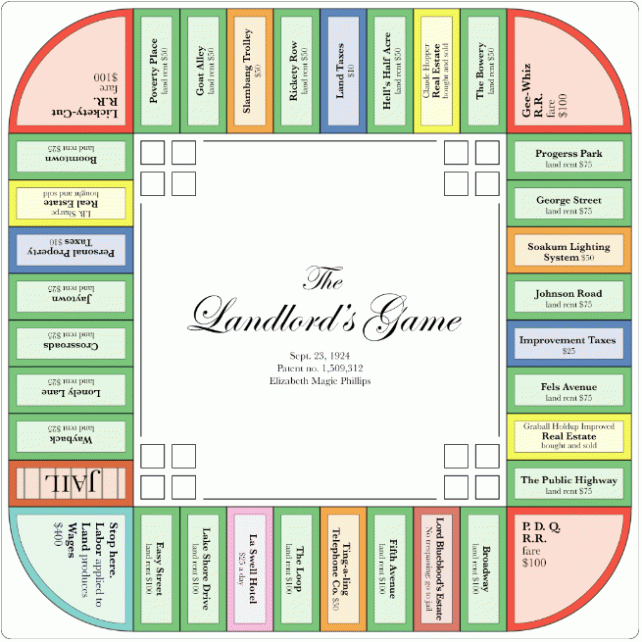
Monopoly, though, has distinctly anticapitalist origins. Its predecessor, The Landlord’s Game, was patented in 1904, in the wake of the Gilded Age, by Elizabeth Magie, a stenographer and typist by trade. Magie was smitten with the ideas of author Henry George, whose 1879 best-seller, Progress and Poverty, had sold millions of copies. Though not a politician, George was the Bernie Sanders or Elizabeth Warren of his day. Among other things, he supported a “land value tax”—a wealth tax meant to curb the power of greedy landlords. Magie hoped her game would educate the public about George’s beliefs.
In her Monopoly precursor, the square we know as “GO” contained a world map and the phrase, “Labor upon Mother Earth produces wages.” Her “Go to Jail” square was a critique of class disparities, reading, “Owner, Lord Blueblood, London England, No Trespassing, Go to Jail.”
Who’d have guessed that two games that underscore the unfairness of our society would become some of our most enduring family pastimes, selling hundreds of millions of sets? We Americans, apparently, are gluttons for punishment.
Above: A mockup from Elizabeth Magie’s original 1904 patent for The Landlord’s Game.
Below: A more polished version, patented in 1924.
Yahtzee probabilities
It’s been ages since I had a math class, so I relied on a pro: friend and neighbor Matthias Beck, a math professor at San Francisco State University. These are his calculations (the asterisk is a multiplication sign, and the 6 represents the six sides of a die). But don’t ask me any further questions, because I don’t get it either…
Let’s assume a player has a very simple strategy, namely they will go for a Yahtzee only when they have three or more equal dice in their first roll. Then the odds of rolling a Yahtzee in a given turn is 6*(5 choose 3)*(1/6)3*(5/6)2*((5/6)2*(1/6)2 + 2*(1/6)*(5/6)*(1/6) + (1/6)2) + 6*5*(1/6)4*(5/6)*(1/6 + (5/6)*(1/6)) + 6*(1/6)5 = 2.47%.
Then the chance of no Yahtzee in 13 turns is (.975)13 = 72%. => the chance to get at least one Yahtzee is 28%.
The chance of exactly one Yahtzee is 13*(.0247)*(.975)12 = 23.7%. => the chance to get at least two Yahtzees is 4.3%.
The chance of exactly two Yahtzees is (13 choose 2)*(.0247)2*(.975)11 = 3.6% => the chance to get at least three Yahtzees is 0.7%.
The chance of exactly three Yahtzees is (13 choose 3)*(.0247)3*(.975)10 = 0.33%. => the chance to get at least four Yahtzees is 0.4%.
Correction: I originally had Beck as a professor at UCSF. Should have been SF State.

















